How a Telescope Works

Introduction

I first became interested in learning more about how telescopes work after I read about adaptive optics, which is a system for correcting a telescope image that has been distorted by non-uniformities of the atmosphere. These distortions are what is happening when we see a star twinkle.

There are two main parts to what I did. In the first part of the project I did two sets of experiments to see what the image size of a distant object like a planet is using just one lens. In the outside experiment I used the sun as the object, and in the inside experiment I used an artificial "planet" (a light bulb across the room). In the second part of the project I combined two lenses to make a complete simple telescope and measured its magnification.

Math Background

Far-away objects in the sky are not measured in centimeters and inches the way we measure everyday nearby objects but are instead measured in terms of angles (degrees or radians). Degrees can be broken down further into minutes (60 minutes = one degree) and seconds (60 seconds = one minute). A circle has a circumference of 360 degrees or 2 pi radians. A radian is just another unit of angular measure, with one radian equaling 360 / (2*π) or approximately 57 degrees.

In the above diagram the angle θ = S/R.   S corresponds to the length around the edge of the circle and R is the radius. When S is the whole circumference (2*π*R), the corresponding θ will be 2π radians (a full 360 degrees).

When working with small angles it helpful to notice that the sine or tangent of an angle expressed in radians can be approximated by just the angle itself.

sin (θ) = tan (θ) = θ

It follows from this that the angular size of a distant object is given by its diameter divided by its distance away from us. For example, for an objective 1 cm wide 100 cm away, the angle is approximately 0.6 degrees. These numbers come from looking at the moon. To us the moon appears to be 1 cm wide 100 cm away.

1 cm / 100 cm = 0.01 radians or 0.57 degrees

Astronomers sometimes use yet another set of units called parsecs which is related to radians and the small-angle approximation.

1 Astronomical Unit (AU) / 1 parsec = 1 arcsecond (in radians)

1 pc = 3.2616 ly (light years)

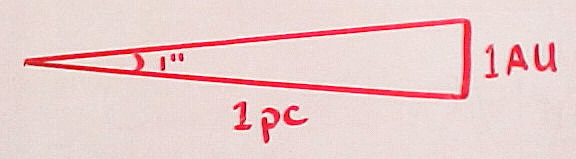
Image Size of a Distant Object (One Lens)

An Important Formula

The image size y of a distant object formed with a single lens is given by:

y   =   f * θ

In this formula f is the focal length of the lens and θ is the angular size of the object, which is given by the object's diameter divided by its distance from us. The formula is derived using the small angle approximation and is only valid if θ is small. The sketch below shows where the formula comes from.

Making an Image of the Sun

The sun appears to have an angular size of 0.53 degree or about 1/100 radian in the sky. This comes from dividing the diameter of the sun (1.39*10^6 km) by its distance from us (1.50*10^8 km). According to the formula above, a lens like a typical "magnifying glass" with a focal length of 10 cm will produce an image of the sun with a diameter of   f * (1/100) = 1 mm. This image is so small that it appears like a point. The lenses in reading glasses have a much longer focal length, so they produce a much larger size image, big enough to appear like a disk. These pictures show focussing sunlight first with a magnifying glass (the paper caught fire!) and then with reading glasses. The focal length of the reading glasses was measured to be 71 cm with the meter stick, and the image size was 7 mm in diameter, exactly as expected.

           

Testing the Formula with an Indoors Experiment

In the lab, Dr. Noé and I set up an experiment to find the image size of an "artifical sun" (an Ott Light) through different lenses. The Ott Light was 5.0 inches high and it was placed on a table 34 feet = 408 inches from the front door. This means its angular size was 0.70 degrees or 0.0122 radians. For each lens the size of the image was estimated by comparing it to boxes on graph paper, and the focal length (the distance where the image was sharpest) was measured with a ruler. The predicted image sizes come from multiplying the angular size of the light source by the measured focal length. They are in good agreement with the measured sizes, especially for the larger size images where the image size can be measured more accurately.

           

Making a Simple Telescope (Two Lenses)

A refracting telescope is made by using two converging lenses separated by a distance equal to the sum of their focal lengths. The first lens (the objective lens) focuses the incoming rays from the planet or moon to a focal plane a set distance away from the lens, the focal length. The light rays converge to form an inverted image in the focal plane and then spread out. A second lens (the eyepiece lens) is used to make the rays parallel once again. In order to magnify the object the objective lens must have a longer focal length than the eyepiece lens. The magnification M is equal to the ratio of the two focal lenths, f(objective) / f(eyepiece).

To try this out I set up an experiment with two simple magnifying lenses. I first found the focal lengths of each lens individually. The objective lens had a focal length of 11.2 inches and the eyepiece lens had a focal length of 3.1 inches. I set up the lenses on a tabletop a distance 14.3 inches apart and moved them around until a distant sign on the door came into view.

The two pictures below show the setup and the view I saw through the telescope. The magnification was estimated by comparing the size of the sign on the door in the picture (in pixels) with and without the telescope, using the program xv. The ratio of the two image sizes was 3.2. This is in pretty good agreement (within 10%) with the ratio of the two focal lengths, which was 3.5.

      

Want to know more?   ....   Try visiting this web page.