Simulating Stellar Imaging in the Optics Laboratory

Introduction:

This project was inspired by an interest in observational astronomy. Its goal is to demonstrate important concepts and techniques of astronomical observation through simple laboratory experiments.

In astronomy, one often works with light from "point sources." These are simply sources of light, like stars, with negligible dimensions compared to their distance from us. A key concept in all types of optical imaging is the point spread function, or PSF, which is the image of a point source created by the optical system. In theory, the PSF of a point source is a point image, but aberrations and diffraction make this impossible to achieve in practice. Aberrations can be eliminated with perfect optics that are perfectly aligned, but diffraction cannot be eliminated, only reduced. As a consequence of diffraction, the PSF for light passed through a circular aperture is an "Airy pattern," a central disk of light surrounded by concentric rings. The size of the pattern is inversely dependent on the aperture; a larger telescope has less diffraction.

Our initial experiment consisted of determining the PSF of a simulated star by imaging it with a consumer camera, the Sony Mavica FD73, at 10X zoom setting. The "star" was created by illuminating a 100 micron pinhole with red light from a HeNe laser. With the camera placed 9.5 m from the pinhole the angular diameter of the "star" is 2.2 arcseconds. While this is still considerably larger than the largest actual star (Betelgeuse, 0.05 arcsec), it is sufficiently small for this experiment.

The figures below show the observed PSF as an expanded image and as a plot of pixel intensity values. The size of each pixel is 5.6x5.6 microns. The PSF is quite symmetric, and only about 2.5 times the estimated diameter of the Airy disk. We can conclude that the optics of the camera are excellent, and its imaging capability is close to the diffraction limit.

In the future we hope to use these results to explore spectroscopy of a simulated star by illuminating the pinhole with light from a spectral lamp and imaging this through a diffraction grating.

Background:

In astronomy, one often deals with light of a "point source". The dimensions of the observed light are negligable when compared to the distance away from the observer the source is. When observed with an optical system, such as a telescope of a camera, the image of the source is a point spread function, PSF. The PSF is caused by diffration and abberation inside the optical system. The light is diffracted when it enters the aperature of the telescope, and further when it moves through the inside of the instrument. Because of this, the image of the light will never be perfect. Theoretically, a PSF of a point source is a single point of light, however with real optical systems this is impossible to achieve.

The diffration pattern for light passing through a circular aperature is an airy pattern. An airy pattern is a central disk surrounded by concentric rings with decreasing intensity. The size of the airy pattern is inversely dependant on the size of the apreature of the instrument. With a smaller opening, the airy pattern of the point will be larger.

Airy pattern and its PSF

Our Optical System:

The number of the ccd element has correspoding dimensions. To find the dimensions, I simply looked it up online and found that the ccd element is 2.7 x 3.6 mm. With a little math it was easy to find the dimensions of each pixel on the ccd element. The element is square with pixels of dimensions 5.625 x 5.625 microns.

When using an optical system to image a point source, the Raleigh Criteria can be used to show the relationship between the size of the diffraction pattern and the properties of the system. In this case, the equation can be used to demonstrate the relationship between the diameter of the airy pattern and the camera lens. The Ralegh Criteria is:

The diameter is the size of the lens aperature when the image is taken. This can be measured, however, sometimes it changes when the camera takes a picture. We concluded, by taking a picture next to a ruler, that when the camera is not zoomed, the lens aperature may close as much as half. This will effect the diameter of the airy pattern on the image.

Setup:

The first goal of the experiment was to create a simulation of a star. To do this, we created a point source but illuminating a 100 micron pinhole with a laser. The pinhole was imaged from across the room with our camera in the very center of the light.

Results:

A picture of the pinhole was taken from ~10 meters away, with the camera zoomed all the way, with the aperature at the center of the airy pattern. The image was taken in the black and white setting, in a compressed jpg format.

The image was uploaded and cropped and greatly magnified so the pixels were easy to see. The intensity values of the PSF were found and graphed in gnuplot, using a simple pattern of numbers.

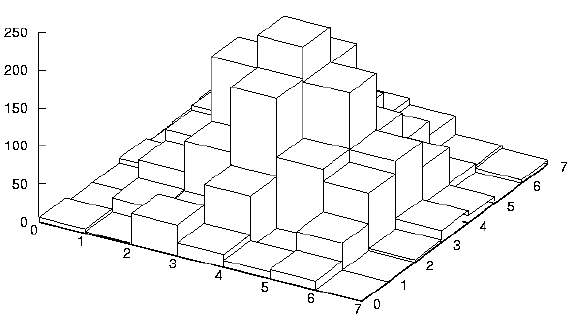
Each level on the plot had to have 4 points describing it, one at each of the corners. Therefore, at each point on the x axis, 4 different levels were described. It was not a complicated pattern, however it was a tedious one to finish. The array is 7x7 pixels, with 4 numbers per pixel. In the end, 196 sets of numbers were needed to create the graph.

Using the information about the camera, the diameter of the airy pattern on the psf was found. Using the zoomed f# of the camera (4), it was assumed that the size of the airy pattern is 2 pixels. This means that it was 2 times the diffraction limit. The airy pattern on the pixels would look like this.

However, these conclusions are based on the idea that the diameter of the lens aperature does not change when a picture is taken. In reality, the lens aperature does change, and therefore the f# is not what we have assumed. If the diameter of the aperature becomes smaller (as we have seen it do), then the diameter of the Airy pattern would be larger. It was concluded that the aperature of the lens may change to as much as 1/2 the original size. This means that the diameter of the Airy pattern would be 2 times larger than if the lens aperature did not change. Therefore we would be at 4 times the diffration limit, not 2.