The Snell's Law method is quite simple. I will take a beam of
light, shine it through a much thinner tank and record the vertical
distance that the light is curved. In other words, the index would be an
average over whatever distance the beam curve travels in the vertical
direction. Intuitivley I thought that this would only be an average index
over the vertical distance; however, Snell's Law states
that n1sin(a1)=n2sin(a2). Elaborating on that, Dr. Noe and I came to
the conclusion that
n1sin(a1)=n2sin(a2)=n3sin(a3)=n4sin(a4)...=nXsin(aX). Therefore
n1sin(a1)=nXsin(aX). This means that we are not in fact averaging over a
long distance as we thought, but we are actually figuring out the index of
refraction of the medium at the level that the beam left the
tank.
Here is a diagram of the setup I used in this experiment :
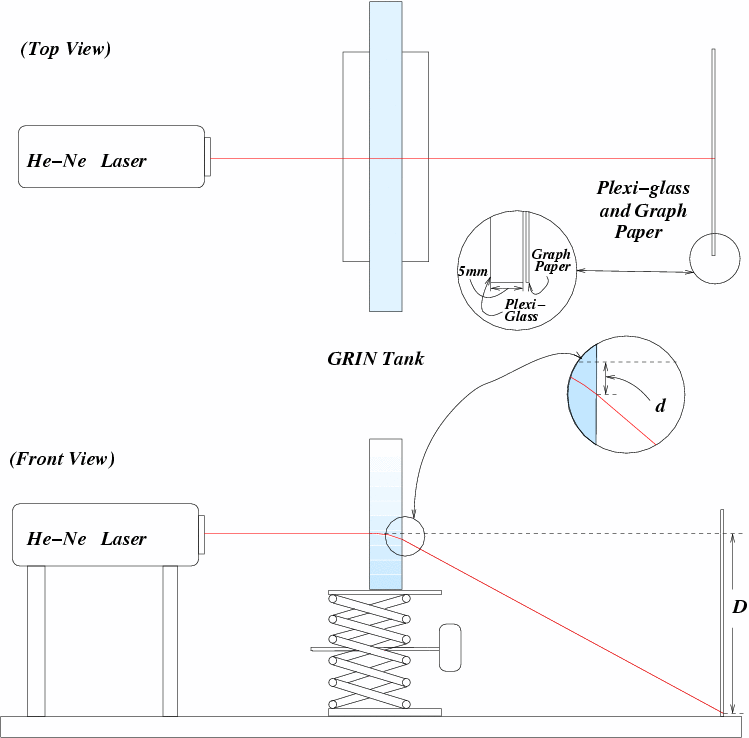
This method proved effective not at measuring a value of the index at a specific depth, but rather as a method of defining the path that light will travel at different levels in the tank. Observing how light behaves with different gradients over the depth of this tank reinforced the fact that the light travels over a parabolic curve.
Pictures





Astro Matt | Home Laser Teaching Center Project Home |